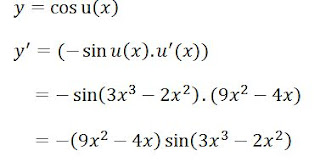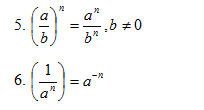Turunan Matematika adalah
Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x dinotasikan dengan :
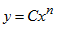 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 
Jika y = C dengan
Jika y = f(x) + g(x) maka
Jika y = f(x).g(x) maka



 . Turunan kedua diperoleh dengan menurunkan turunan pertama.
. Turunan kedua diperoleh dengan menurunkan turunan pertama.
Contoh :
Misalkan y adalah fungsi dari x atau y = f(x). Turunan (atau diferensial) dari y terhadap x dinotasikan dengan :

Rumus Turunan dan contoh
Jika 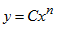 dengan C dan n konstanta real, maka :
dengan C dan n konstanta real, maka : 
Jika y = C dengan

Jika y = f(x) + g(x) maka

Jika y = f(x).g(x) maka




Turunan Kedua
Turunan kedua y = f(x) terhadap x dinotasikan dengan  . Turunan kedua diperoleh dengan menurunkan turunan pertama.
. Turunan kedua diperoleh dengan menurunkan turunan pertama. Contoh :