Jenis-jenis transformasi yang dapat dilakukan antara lain :
- Translasi (Pergeseran)
- Refleksi (Pencerminan)
- Rotasi (Perputaran)
- Dilatasi (Perkalian)
1. Translasi
Translasi (pergeseran) adalah pemindahan suatu objek sepanjang garis lurus dengan arah dan jarak tertentu.
Jika translasi memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
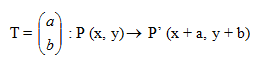
Contoh : Tentukan koordinat bayangan titik A (-3, 4) oleh translasi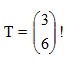
Jawab :
2. Refleksi
a. Pencerminan terhadap sumbu x
b. Pencerminan Terhadap sumbu y
c. Pencerminan terhadap garis y = x
d. Pencerminan terhadap garis y = -x
e. Pencerminan terhadap garis x = h
f. Pencerminan terhadap garis y=k
g. Pencerminan terhadap titik asal O (0, 0)
h. Pencerminan terhadap garis y = mx dimana m = tan q
3. Rotasi
Ket.: Ciri khas suatu matriks Rotasi adalah determinannya = 1
SIFAT-SIFAT
Jika translasi
 memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk :
memetakan titik P (x, y) ke titik P’(x’, y’) maka x’ = x + a dan y’ = y + b atay P’ (x + a, y + b ) ditulis dalam bentuk : 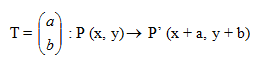
Contoh : Tentukan koordinat bayangan titik A (-3, 4) oleh translasi
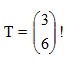
Jawab :
2. Refleksi
a. Pencerminan terhadap sumbu x
b. Pencerminan Terhadap sumbu y
c. Pencerminan terhadap garis y = x
d. Pencerminan terhadap garis y = -x
e. Pencerminan terhadap garis x = h
f. Pencerminan terhadap garis y=k
g. Pencerminan terhadap titik asal O (0, 0)
h. Pencerminan terhadap garis y = mx dimana m = tan q
3. Rotasi
rotasi | matriks | perubahan titik | perubahan fungsi |
½ p | é0 -1ù ë1 -0 û | (x,y) ® (-y,x) | F(x,y) = 0 ® F(y,-x) = 0 |
p | é-1 0ù ë1 -1 û | (x,y) ® (-x,-y) | F(x,y) = 0 ® F(-x,-y) = 0 |
3/2 p | é0 -1ù ë-1 0 û | (x,y) ® (y,-x) | F(x,y) = 0 ® F(-y,x) = 0 |
q | écosq -sinq ù ësinq cosq û | (x,y) ® (x cos q - y sinq, x sin q + y cos q) F(x,y) = 0 ® F(x cos q + y sin q, -x sin q + y cos q) = 0 | |
Ket.: Ciri khas suatu matriks Rotasi adalah determinannya = 1
SIFAT-SIFAT
- Dua rotasi bertumt-turut mempakan rotasi lagi dengan sudut putar dsama dengan jumlah kedua sudut putar semula.
- Pada suatu rotasi, setiap bangun tidak berubah bentuknya.
Catatan:
Pada transformasi pergeseran (translasi), pencerminan (refleksi) dan perputaran (rotasi), tampak bahwa bentuk bayangan sama dan sebangun (kongruen) dengan bentuk aslinya. Transformasi jenis ini disebut transformasi isometri.
- DilatasiMatriksPerubahan titikPerubahan fungsi(0,k)ék 0ù
ë0 kû(x,y)®(kx,ky)F(x,y)=0®F(x/k,y/k)
Ket.:
(0, k) merupakan perbesaran atau pengecilan dengan tergantung dari nilai k.
Jika A' adalah peta dari A, maka untuk:a. k > 1 ® A' terletak pada perpanjangan OAb. 0 < k < 1 ® A' terletak di antara O dan Ac. k > 0 ® A' terletak pada perpanjangan AO
- TRANSFORMASI LINIER
Ditentukan oleh matriks éa bù
ëc dû
é x'ù = é a b ù é x
ù
ë y' ûë c d û ë y û
é xù = 1
é a -b ù é x'
ù
ë y û ad - bc ë -c d û ë y' û
Perubahan TitikPerubahan Fungsi(x,y)®(ax+by, cx+dy)F(x,y)=0 ® édx - by , -cx + ay ù
ëad - bc ad - bcû
Prinsipnya adalah mencari matriks invers dari matriks transformasi yang diketahui.




























seharusnya itu dikasih contoh soal biar tambah jelas..
ReplyDelete